Binary Search Tree
Post By kanra
Blogs Binary Search Tree
March 20, 2019
Category
Data Structure
Tag
AlgorithmC++

This post containing some libraries, reusable functions and structs for Binary Search Tree (BST).

 

Binary Tree

A tree in which each node has at most two children

 

Balanced Binary Tree

Left subtree of T is balanced
Right subtree of T is balanced
The difference between heights of left subtree and right subtree is not more than 1.

 

Complete Binary Tree

A binary tree is considered to be completed if it is full until 2nd last level, and it has leave that is full from left to right.
A completed BST is balanced.

 

Full Binary Tree

A binary tree of height h whose leaves are all at the level h and whose nodes all have two children; this is considered to be completely balanced.
A full BST is balanced.
A full BST is complete.

 

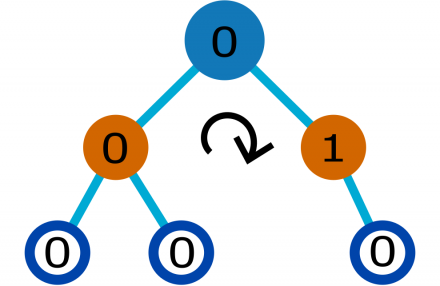
Binary Search Tree

A sorted binary tree, according to the key values in the nodes. Like below.

 

Binary Search Tree

 

 

Abstract Data Type (ADT)

// BST tree type node
template<class Type>
struct node_t
{
	Type data;
	node_t<Type> *left;
	node_t<Type> *right;
};

 

Get the size of a BST

template<class Type>
int BST_size(node_t<Type> * root)
{
	return ((root) ? 1 + BST_size(root->left) + BST_size(root->right) : 0);
}

 

Get the height of a BST

template<class Type>
int BST_height(node_t<Type> * root)
{
	if (root)
	{
		int left = BST_height(root->left);
		int right = BST_height(root->right);
		if (left > right)
			return ++left;
		else
			return ++right;
	}

	return 0;
}

 

Clear a BST

// Return number of node deleted
template<class Type>
int BST_clear(node_t<Type>* &root)
{
	int count = 0;
	if (root)
	{
		count = BST_clear(root->left) + BST_clear(root->right) + 1;

		delete root;
		root = NULL;
	}

	return count;
}

 

Display items by value in order for a BST

// Return number of node displayed
template<class Type>
int BST_display(node_t<Type>* root)
{
	int count = 0;
	if (root)
	{
		count += BST_display(root->left);
		cout << root->data << " "; ++count; count += BST_display(root->right);
	}

	return count;
}

 

Display a Tree like graph

/*
output:
               191
          169 <
               161
     144 <
          137 \
               124
120 <
     83 \
               35
          34 <
               11
*/
// Declaration
template<class Type>
int BST_dis(node_t<Type> *root, int lv =1);

template<class Type>
int BST_dis(node_t<Type> *root, int lv)
{
	int cc = 0;
	if (root)
	{
		cc = BST_dis(root->right, lv + 1) + 1;
		int sp = lv;
		while (sp-- > 1)
		{
			cout << "     ";
		}
		cout << root->data
		    << ((root->left && root->right) ? " < " : ((root->right) ? " / " : ((root->left) ? " \\ " : ""))) 
		    << endl; 
		cc += BST_dis(root->left, lv + 1);
	}

	return cc;
}

 

Insert into a BST by value as a leaf

// return the level of this new node in the BST
template<class Type>
int BST_insert(const Type &to_insert, node_t<Type>* &root)
{
	if (root)
	{
		if (to_insert < root->data)
			return BST_insert(to_insert, root->left) + 1;
		else
			return BST_insert(to_insert, root->right) + 1;
	}
	else
	{
		root = new node_t<Type>;
		root->data = to_insert;
		root->left = root->right = NULL;
	}

	return 1;
}

 

Remove item by value in a BST

Using a helper function to maintain the BST after removing a node.
Finding the inorder successor of the removed node and replace the node to be removed with it.
Then remove the inorder successor.

// Return whether removal is successfully
template<class Type>
bool BST_remove(const Type &to_remove, node_t<Type>* &root)
{
	if (root)
	{
		if (to_remove == root->data)
		{
			if (root->left && root->right)
				BST_remove_supply_smallest(root->data, root->right);
			else if (!root->left && !root->right)
			{
				delete root;
				root = NULL;
			}
			else
			{
				node_t<Type> *del = root;
				root = ((root->left) ? root->left : root->right);
				delete del;
			}

			return true;
		}
		else if (to_remove < root->data)
			return BST_remove(to_remove, root->left);
		else
			return BST_remove(to_remove, root->right);
	}

	return false;
}

// Remove the smallest item and supply it back by parameter
// Return whether there is a node removed
template<class Type>
int BST_remove_supply_smallest(Type &receive, node_t<Type>* &root)
{
	if (root)
	{
		if (root->left)
			return BST_remove_supply_smallest(receive, root->left);
		else
		{
			node_t<Type>* del = root;
			receive = root->data;
			root = root->right;
			delete del;
			return 1;
		}
	}

	return 0;
}

 

Make a complete copy of BST

// dest is the destination BST
// source is the source BST to be copied
template<class Type>
int BST_copy(node_t<Type>* &dest, node_t<Type>* source)
{
	int count = 0;
	if (source)
	{
		dest = new node_t<Type>;
		dest->data = source->data;

		count = BST_copy(dest->left, source->left) + BST_copy(dest->right, source->right) + 1;
	}
	else
		dest = NULL;

	return count;
}

 

Determine if a BST is height-balanced tree

// Returns true is balanced
template<class Type>
bool BST_is_balanced(node_t<Type> *root)
{
	int lh;			/* for height of left subtree */
	int rh;			/* for height of right subtree */

	/* If tree is empty then return true */
	if (root == NULL)
		return 1;

	/* Get the height of left and right sub trees */
	lh = BST_height(root->left);
	rh = BST_height(root->right);

	int differ = lh - rh;

	// The difference of heights of left subtree and right subtree is not more than 1.
	if ((differ == 1 || differ == 0 || differ == -1) && 
		BST_is_balanced(root->left) && 
		BST_is_balanced(root->right))
		return 1;

	/* The tree is not height-balanced here */
	return 0;
}

 

Determine if a BST is a completed BST

// Return true is completed
template<class Type>
bool BST_is_complete(node_t<Type>* root)
{
	if (root)
	{
		int largest_index = 0;
		int  cc = BST_is_complete(root, largest_index, 0);
		return (((largest_index) < cc) ? 1 : 0);
	}

	return 0;
}

/*
Recursive helper function to determine if a BST is a completed BST
*/
template<class Type>
int BST_is_complete(node_t<Type>* root, int &index, int local_index)
{
	if (root)
	{
		if(local_index > index)
			index = local_index;

		// Recur for left and right subtrees
		return (BST_is_complete(root->left, index, 2 * local_index + 1) +	
            BST_is_complete(root->right, index, 2 * local_index + 2)) + 1;
	}

	return 0;
}

 

Determine if a BST is a full BST

template<class Type>
bool BST_is_full(node_t<Type>* root)
{
	if (root)
	{
		if (root->left && root->right)
			return ((BST_is_full(root->left)) ? (BST_is_full(root->right) ? 1 : 0) : 0);
		else if (!root->left && !root->right)
			return 1;
		else
			return 0;
	}
	return 0;
}

 

Count duplicated elements

For elements 1 2 3 4 4 5 5 5 6 6, number of duplicated elements is 4.

// Declaration
template<class Type>
int count_d(node_t<Type> *root, node_t<Type> *last = 0);

template<class Type>
int count_d(node_t<Type> *root, node_t<Type> *last)
{
	int count = 0;
	if (root)
	{
		count = count_d(root->left, last);
		if (last && last->data == root->data)
			++count;
		else
			last = root;

		count += count_d(root->right, last);
	}

	return count;
}

 

Remove the largest element

1 4 5 8 9 15 19, remove 19

template<class Type>
int remove_largest(node_t<Type> *&root)
{
	int la = 0;
	if (root)
	{
		if (root->right)
		{
			la = remove_largest(root->right);
			if (root->data == la)
			{
				node_t<Type> *temp = root->left;
				delete root;
				root = temp;
			}
		}
		else
		{
			la = root->data;
			node_t<Type> *temp = root->left;
			delete root;
			root = temp;
		}
	}

	return la;
}

 

Remove the 2nd largest element

1 4 5 8 9 15 19, remove 15

template<class Type>
int remove_2nd_largest(node_t<Type> *&root)
{
	int la = 0, se = 0;
	return remove_2nd_largest(root, la, se);
}

// recursive helper fnc for removing the 2nd largest element
template<class Type>
int remove_2nd_largest(node_t<Type> *&root, int &largest, int& second)
{
	int cc = 0;
	if (root)
	{
		cc = remove_2nd_largest(root->right, largest,second);

		if (!largest)
		{
			largest = root->data;
		}
		else if ((!second && largest > root->data) || (second && second == root->data))
		{
			second = root->data;
			if (root->right)	// right is largest
			{
				node_t<Type> *del = root;
				if(root->left)
					root->right->left = root->left;
				root = root->right;
				delete del;
			}
			else
			{
				node_t<Type> *del = root;
				root = root->left;
				delete del;
			}
			++cc;
		}

		if( !second || (second && root && root->left && root->left->data == second))
			cc += remove_2nd_largest(root->left,largest,second);
	}
	return cc;
}

 

Remove the largest 2 elements

1 4 5 8 9 15 19, remove 15 and 19

// Return # of elements removed
template<class Type>
int remove_largest2(node_t<Type> *& root)
{
	int *cc = new int(0);
	remove_largest2(root, cc);
	return *cc;
}

// recursive helper fnc for removing the largest 2 elements
template<class Type>
int remove_largest2(node_t<Type> *&root, int *cc)
{
	int c = 0;
	if (root)
	{
		c = remove_largest2(root->right, cc);

		if (!root->right && *cc <2) { 
			node_t<Type>* temp = root->left;
			delete root;
			root = temp;
			++(*cc);
			if (root)
				return remove_largest2(root, cc);
		}

		if (*cc <2 && root) return remove_largest2(root->left, cc);
	}

	return c;
}

 

Copy even elements of a BST to a new BST

// Return # of elements copied
template<class Type>
int copy_even(node_t<Type> *&root1, node_t<Type> *root2)
{
	if (root2)
	{
		if (root2->data % 2 == 0)
		{
			if (root1)
			{
				BST_insert(root2->data,root1 );
				return copy_even(root1, root2->left) + copy_even(root1, root2->right) + 1;
			}
			else
			{
				BST_insert(root2->data,root1);
				return copy_even(root1->left, root2->left) + copy_even(root1->right, root2->right) + 1;
			}
		}
		else
			return copy_even(root1, root2->left) + copy_even(root1, root2->right);
	}
	return 0;
}

 

Copy all leave of a BST to a new BST

// Declaration
template<class Type>
int copy_leaf(node_t<Type> *&root1, node_t<Type> *root2, int swap = 0);

// Return # of elements copied
template<class Type>
int copy_leaf(node_t<Type> *&root1, node_t<Type> *root2, int swap)
{
	if (root2)
	{
		if (!root2->left && !root2->right)
		{
			if (root1)
			{
				BST_insert(root2->data, root1);
				return copy_leaf(root1, root2->left) + copy_leaf(root1, root2->right) + 1;
			}
			else
			{
				BST_insert(root2->data, root1);
				return copy_leaf(root1->left, root2->left) + copy_leaf(root1->right, root2->right) + 1;
			}
		}
		else
		{
			if(swap)
				return copy_leaf(root1, root2->left, 0) + copy_leaf(root1, root2->right, 0);
			else
				return copy_leaf(root1, root2->right,1) + copy_leaf(root1, root2->left,1);
		}

	}
	return 0;
}

 

Remove all even elements of a BST

template<class Type>
int BST_remove_even(node_t<Type> *&root)
{
	int cc = 0;
	if (root)
	{
		cc += BST_remove_even(root->left);
		cc += BST_remove_even(root->right);
		if ((root->data % 2) == 0)
		{
			if (root->left && root->right)
				BST_remove_supply_smallest(root->data, root->right);
			else if (!root->left && !root->right)
			{
				delete root;
				root = NULL;
			}
			else
			{
				node_t<Type> *del = root;
				root = ((root->left) ? root->left : root->right);
				delete del;
			}

			++cc;
		}
	}
	return cc;
}

 

Search a BST for a range of elements

// This function display element in a range
// return # of elements in a range
template<class Type>
int BST_search(node_t<Type> *root, int max, int min)
{
	bool f = 0, p =0;
	return BST_search(root, max, min, f, p);
}

// recursive helper fnc for searching elements in a range 
template<class Type>
int BST_search(node_t<Type> *root, int max, int min, bool &found, bool &pass)
{
	int cc = 0;
	if (root)
	{
		if (min < root->data)
			cc = BST_search(root->left, max, min, found, pass);

		if (!pass &&  min <= root->data  && root->data <= max)
		{
			++cc;
			found = 1;
			cout << root->data << " "; 
			cc += BST_search(root->right, max, min, found, pass);

		}
		else if (found)
		{
			pass = 1;
		}
		else	if(max >= root->data)
			cc += BST_search(root->right, max, min, found, pass);
	}
	return cc;
}

 

Reverse an in-order BST to reversed order

// 1 2 3 => 3 2 1
// return # of element
template<class Type>
int BST_reverse(node_t<Type> *root)
{
	int cc = 0;
	if (root)
	{
		cc = BST_reverse(root->left) + BST_reverse(root->right) + 1;

		node_t<Type> *temp = root->right;
		root->right = root->left;
		root->left = temp;
	}

	return cc;
}

 

Duplicate all elements except root node

// Return # of elements duplicated
template<class Type>
int BST_duplicate_all(node_t<Type> *root, node_t<Type> *ro)
{
	int cc = 0;
	if (root)
	{
		cc = BST_duplicate_all(root->left, ro) + BST_duplicate_all(root->right, ro) + 1;
		
		if (root != ro)
			add_to_left(root->right, root->data);
	}
	return cc;
}

// Recursive helper function for duplicating all elements except root node
template<class Type>
int add_to_left(node_t<Type> *&root, int data)
{
	if (root)
		return add_to_left(root->left, data);
	else
	{
		root = new node_t<Type>;
		root->data = data;
		root->right = root->left = 0;
	}
	return 1;
}

 

AUTHOR : kanra
EMAIL : karawakara@gmail.com
Working on Networking, Web Development, Software Development, Server-side deployment. Having fun on doing experiments on new technologies.
Related Posts