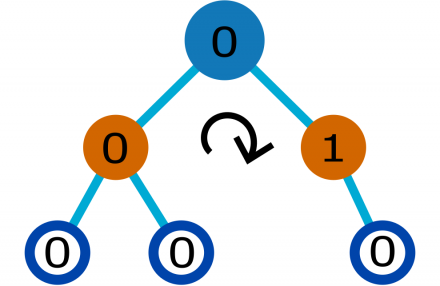
Abstract Data Type (ADT)
template<class type>
struct node23
{
type *data[2];
node23<Type> *child[3]; // max 3 children
};
Get number of node in a 2-3 tree
template<class type>
int Tree23_size(node23<Type>* root)
{
return ((root) ? Tree23_size(root->child[0]) + Tree23_size(root->child[1]) +
Tree23_size(root->child[2]) + 1 : 0);
}
Get number of data in a 2-3 tree
template<class type>
int Tree23_data(node23<Type>* root)
{
int data = 0;
if (root)
{
if (root->data[1])
data = Tree23_data(root->child[0]) + Tree23_data(root->child[1])
+ Tree23_data(root->child[2]) + 2;
else
data = Tree23_data(root->child[0]) + Tree23_data(root->child[1])
+ Tree23_data(root->child[2]) + 1;
}
return data;
}
Determine whether the height is balanced
template<class type>
bool Tree23_is_balanced(node23<Type> * root)
{
bool is_balanced = 1;
Tree23_is_balanced(root, is_balanced);
return is_balanced;
}
// Recursion function for Tree23_is_balanced
template<class type>
int Tree23_is_balanced(node23<Type> * root, bool & is_balanced)
{
if (root)
{
if (root->data[1])
{
int fi = Tree23_is_balanced(root->child[0], is_balanced);
int se = Tree23_is_balanced(root->child[1], is_balanced);
int th = Tree23_is_balanced(root->child[2], is_balanced);
if (is_balanced)
if (!(fi == se && se == th))
is_balanced = 0;
return fi + 1;
}
else
{
int fi = Tree23_is_balanced(root->child[0], is_balanced);
int se = Tree23_is_balanced(root->child[1], is_balanced);
if (is_balanced)
if (fi != se)
is_balanced = 0;
return fi + 1;
}
}
return 0;
}
Determine whether the data in the tree is in order
template<class type>
int Tree23_data_in_order(node23<Type> * root)
{
if (root)
{
type* prev = NULL;
return Tree23_data_in_order(root, prev);
}
return 1;
}
// Recursive fnc for testing whether the data in the tree is in order
template<class type>
bool Tree23_data_in_order(node23<Type> * root, type *& prev)
{
if (root)
{
if (root->child[0])
if (!Tree23_data_in_order(root->child[0], prev))
return 0;
if (!prev)
prev = root->data[0];
if (*prev > *(root->data[0]))
return 0;
if (root->child[1])
if (!Tree23_data_in_order(root->child[1], prev))
return 0;
if (root->data[1])
{
if (*prev > *(root->data[1]))
return 0;
if (root->child[1])
if (!Tree23_data_in_order(root->child[2], prev))
return 0;
}
}
return 1;
}
Get level of tree height
template<class type>
int Tree23_height(node23<Type> * root)
{
return ((root) ? Tree23_height(root->child[0]) + 1 : 0);
}
Display data of 2-3 tree in order
// Return # of nodes
template<class type>
int Tree23_display(node23<Type> * root)
{
int count = 0;
if (root)
{
if(root->child[0])
count = Tree23_display(root->child[0]);
cout << *(root->data[0]) << " "; if (root->child[1])
count += Tree23_display(root->child[1]);
if (root->data[1]) // 2nd data exist
{
cout << *(root->data[1]) << " "; count += Tree23_display(root->child[2]);
}
++count;
}
return count;
}
Display data in a tree-liked sturcture
// Declaration
template<class type>
int Tree23_display_tree(node23<Type> *root, int lv = 1);
// Return # of data
template<class type>
int Tree23_display_tree (node23<Type> *root, int lv)
{
int data = 0;
if (root)
{
if (root->child[2])
data += Tree23_display_tree(root->child[2], lv + 1); // root is not NULL, data + 1
if (root->data[1])
{
++data;
int sp = lv;
while (sp-- > 1)
cout << " ";
cout << *(root->data[1]) << ((root->child[1]) ? " < " : "") << endl;
}
if (root->child[1])
data += Tree23_display_tree(root->child[1], lv + 1);
int sp = lv;
while (sp-- > 1)
cout << " ";
cout << *(root->data[0]) << ((root->child[0]) ? " < " : "") << endl;
++data;
if (root->child[0])
data += Tree23_display_tree(root->child[0], lv + 1);
}
return data;
}
Clear a 2-3 tree
template<class type>
int Tree23_clear(node23<Type> * &root)
{
int count = 0;
if (root)
{
count = Tree23_clear(root->child[0]) + Tree23_clear(root->child[1]) +
Tree23_clear(root->child[2]) + 1;
delete root->data[0];
if (root->data[1])
delete root->data[1];
delete root;
root = NULL;
}
return count;
}
Make a completed copy of a 2-3 tree
template<class type>
int Tree23_copy(node23<Type> * &dest_root, node23<Type> * source_root)
{
if (source_root)
{
dest_root = new node23<Type>;
dest_root->data[0] = source_root->data[0];
dest_root->data[1] = ((source_root->data[1]) ? source_root->data[1] : 0);
return Tree23_copy(dest_root->child[0], source_root->child[0]) +
Tree23_copy(dest_root->child[1], source_root->child[1]) +
Tree23_copy(dest_root->child[2], source_root->child[2]) + 1;
}
else
dest_root = NULL;
return 0;
}
Insert a data into 2-3 tree
There are 4 functions for this operations:
1. Wrapper function of insertion, also for growth of tree.
- If there is a data pushed up to this point, then root node to grows up 1 level.
2. Recursive function of insertion traversal. Process:
- Start from root, going down to a leaf.
- Insert at a leaf node
- If there are 3 data in a leaf node, push up the middle to its parent.
- If there is 1 data in parent, insert the pushed data, split that child.
- If there are 2 data in parent, split parent into two subtrees, push up middle data.
- Keep pushing until the top
- Tree grows from the top
3. Splitting function to split a child node from a parent node.
- Return NULL if it is done splitting up to this point
- Return the middle value data to its parent ( It is a new right child of node to the parent that is already splited )
4. Inserting function to insert a data into a node of 2-3 tree.
- Return NULL if there is no need to split
- Return a middle value data to parent ( a new right child (already splited) of node to parent )
//Return NULL
template<class type>
type* Tree23_insert(const type & insert, node23<Type>*& root)
{
node23<Type>* below_child = NULL;
type* to_insert = Tree23_insert_traverse(insert, root, below_child);
if (to_insert)
{
node23<Type>* new_root = new node23<Type>;
new_root->data[0] = to_insert;
new_root->child[0] = root;
new_root->child[1] = below_child;
new_root->child[2] = NULL;
new_root->data[1] = NULL;
root = new_root;
}
return NULL;
}
// Return a data pushed up
template<class type>
type* Tree23_insert_traverse(const type & insert, node23<Type>*& root, node23<Type>* &new_child)
{
if (root)
{
if (!root->child[0]) // root is leaf, try to insert
{
type * move_up = Tree23_insert_at_node(insert, root, new_child);
return move_up;
}
else // not leaf, going down
{
node23<Type> *below_child = NULL;
if (insert < *(root->data[0])) // go left
{
type* pushed_data = Tree23_insert_traverse(insert, root->child[0], below_child);
if (pushed_data)
return Tree23_split(root, pushed_data,0, below_child, new_child); // data was pushed from 1st child
}
else if (!(root->data[1]) || insert < *(root->data[1])) // go middle
{
type* pushed_data = Tree23_insert_traverse(insert, root->child[1], below_child);
if (pushed_data)
return Tree23_split(root, pushed_data, 1, below_child, new_child); // data was pushed from 2nd child
}
else // go right
{
type* pushed_data = Tree23_insert_traverse(insert, root->child[2], below_child);
if (pushed_data)
return Tree23_split(root, pushed_data, 2, below_child, new_child); // data was pushed from 3rd child
}
return NULL; // no data was pushed up
}
}
else // root is NULL, 1st node
{
return Tree23_insert_at_node(insert, root, new_child);
}
}
// Return a data pushed up
template<class type>
type* Tree23_split(node23<Type>*& root, type * to_insert, int child_num, node23<Type> *below_child, node23<Type> *& new_child )
{
if (!root->data[1]) // parent node has 1 data
{
if (child_num == 0) // data from child 0
{
root->data[1] = root->data[0];
root->data[0] = to_insert;
root->child[2] = root->child[1];
root->child[1] = below_child;
}
else // data from child 1
{
root->data[1] = to_insert;
root->child[2] = below_child;
}
return NULL;
}
else // parent node has 2 data
{
type* move_up = NULL;
if (child_num == 0) // data from child 0
{
new_child = new node23<Type>;
new_child->child[2] = NULL;
new_child->data[1] = NULL;
new_child->data[0] = root->data[1];
new_child->child[1] = root->child[2];
new_child->child[0] = root->child[1];
root->child[1] = below_child;
root->child[2] = NULL;
root->data[1] = NULL;
move_up = root->data[0]; // push up data 1
root->data[0] = to_insert;
}
else if(child_num == 1) // data from child 1
{
new_child = new node23<Type>;
new_child->child[2] = NULL;
new_child->data[1] = NULL;
new_child->data[0] = root->data[1];
new_child->child[1] = root->child[2];
new_child->child[0] = below_child;
root->child[2] = NULL;
root->data[1] = NULL;
move_up = to_insert; // push up inserted data
}
else // data from child 2
{
new_child = new node23<Type>;
new_child->child[2] = NULL;
new_child->data[1] = NULL;
new_child->data[0] = to_insert;
new_child->child[1] = below_child;
new_child->child[0] = root->child[2];
root->child[2] = NULL;
move_up = root->data[1]; // push up data 2
root->data[1] = NULL;
}
return move_up;
}
}
// Return a data pushed up
template<class type>
type* Tree23_insert_at_node(const type & insert, node23<Type>*& root, node23<Type>*& new_child)
{
if (root)
{
if (insert < *(root->data[0]))
{
if (root->data[1]) // node has 2 data, move up 1st data
{
new_child = new node23<Type>;
new_child->child[0] = new_child->child[1] = new_child->child[2] = NULL;
new_child->data[1] = NULL;
type* move_up = root->data[0];
root->data[0] = new type;
*(root->data[0]) = insert;
new_child->data[0] = root->data[1]; // 2nd data (large) move to new child node
root->data[1] = NULL;
return move_up;
}
else // node has 1 data, insert at 1st
{
root->data[1] = root->data[0];
root->data[0] = new type;
*(root->data[0]) = insert;
}
}
else
{
if (root->data[1]) // node has 2 data, move up middle data
{
new_child = new node23<Type>;
new_child->child[0] = new_child->child[1] = new_child->child[2] = NULL;
new_child->data[1] = NULL;
type* move_up;
if (insert < *(root->data[1])) // move up insert data
{
move_up = new type;
*(move_up) = insert;
new_child->data[0] = root->data[1]; // 2nd data (large) move to new child node
root->data[1] = NULL;
}
else // move up 2nd data
{
new_child->data[0] = new type;
*(new_child->data[0]) = insert; // inserted data (large) move to new child node
move_up = root->data[1];
root->data[1] = NULL;
}
return move_up;
}
else // node has 1 data, insert at 2nd
{
root->data[1] = new type;
*(root->data[1]) = insert;
}
}
}
else // 1st node
{
root = new node23<Type>;
root->data[0] = new type;
*(root->data[0]) = insert;
root->data[1] = NULL;
root->child[0] = root->child[1] = root->child[2] = NULL;
}
return NULL; // done on insert
}
Delete a data from a 2-3 tree
Process:
1. Find the first data to be deleted.
2. If it is a parent node, replace it with the left most of its right subtree.
3. If it is a leaf node, and contain 2 data, done.
4. Else, back to parent, do data redistribution.
5. If that is still not worked, back to next parent, do node merging.
There are 5 functions for this operations:
1. Wrapper function containing an indicator to do nodes redistribution and nodes merging.
2. Recursive traversal function.
3. Remove and supply a smallest inorder successor.
4. Redistribute function for redistributing the data between this parent and its leave data. Cases:
- Child 0 is empty, then
move data 0 down
move child 1 up
move data 1 down
move child 2 up - Child 1 is empty, then
check out child 0
then check parent data 1
then check child 2 - Child 2 is empty, then
only need to check child 1
5. Merging function for merging nodes. Cases:
- Merge node from child 0 if
– child 1 is 2 data
– parent is 2 data
– child 1 and parent is 1 data - Merge node from child 1 if
– child 0 is 2 data
– parent is 2 data
– child 0 and parent is 1 data - Merge node from child 2 if
– child 1 is 2 data
– child 1 is 1 data
// Return if it succeed to delete a target data
template<class type>
bool Tree23_delete(const type & to_delete, node23<Type>*& root)
{
bool done = 0; // indicate whether redistribution and merging are done for rebalancing the tree
return Tree23_delete(to_delete, root, root, done);
}
/*
Recursive function of tree23 delete
Return if it succeed to delete a target data
*/
template<class type>
bool Tree23_delete(const type & to_delete, node23<Type>*& root, node23<Type> *& parent, bool &done)
{
bool result = 0;
if (root)
{
if (to_delete == *(root->data[0])) // to be deleted in data 0
{
result = 1;
if (root->child[1]) // node to be deleted is a parent node
{
done = Tree23_remove_supply_smallest(root->data[0], root->child[1], root);
// at least the distribution had done, or more merge had done on this root node
// root as the parent, had done a merge, here will need to do once before back to previous level
if (!done) // had a data deleted, not done, only do node merging
done = Tree23_merge(parent, root);
}
else // data to be deleted is in a leaf node
{
if (root->data[1]) // 2 data in this node,
{
delete root->data[0];
root->data[0] = root->data[1];
root->data[1] = NULL;
done = 1;
}
else // 1 data in this leaf node
{
delete root->data[0];
root->data[0] = NULL;
done = Tree23_data_distribute(parent); // 0 data in this node, do data distribution on parent
}
}
}
else if (root->data[1] && to_delete == *(root->data[1])) // to be deleted in data 1
{
result = 1;
if (root->child[1]) // node to be deleted is a parent node
{
done = Tree23_remove_supply_smallest(root->data[1], root->child[2], root);
// at least the distribution had done, or more merge had done on this root node
}
else // data to be deleted is in a leaf node, 2 data in this node
{
delete root->data[1];
root->data[1] = NULL;
done = 1;
}
}
else if (to_delete < *(root->data[0])) // go left
{
result = Tree23_delete(to_delete, root->child[0], root, done);
if (result && !done) // had a data deleted, not done, only do node merging
done = Tree23_merge(parent, root);
}
else if(!(root->data[1]) || to_delete < *(root->data[1])) // go middle
{
result = Tree23_delete(to_delete, root->child[1], root, done);
if (result && !done) // had a data deleted, not done, only do node merging
done = Tree23_merge(parent, root);
}
else // go right
{
result = Tree23_delete(to_delete, root->child[2], root, done);
if (result && !done) // had a data deleted, not done, only do node merging
done = Tree23_merge(parent, root);
}
}
return result;
}
/*
Remove the smallest item and supply it back by parameter
replace with the left most node of the root's right subtree (take out 1 from right)
Return whether all the works has been done
*/
template<class type>
bool Tree23_remove_supply_smallest(type *&receive, node23<Type>* &root, node23<Type> *& parent)
{
if (root)
{
if (root->child[0])
{
bool done = Tree23_remove_supply_smallest(receive, root->child[0], root);
if (!done) // distribution still not work, or after one or more merge still not work
return Tree23_merge(parent, root); // do node merging
return done;
}
else // end leaf
{
delete receive;
receive = root->data[0];
root->data[0] = NULL;
if (root->data[1]) // 2 data in this node
{
root->data[0] = root->data[1];
root->data[1] = NULL;
return 1;
}
return Tree23_data_distribute(parent); // 1 data in this node, do data distribution on parent
}
}
return 0;
}
/*
Redistribute the data between this parent and its leave data
One of its three children is empty when call this fnc
return 1 if is done here
return 0 if not done yet
Return whether all the works has been done
*/
template<class type>
bool Tree23_data_distribute(node23<Type>* &parent)
{
if (parent->child[0]) // has children
{
if (!(parent->child[0]->data[0])) // child 0 is empty
{
parent->child[0]->data[0] = parent->data[0]; // move data-0 down
parent->data[0] = parent->child[1]->data[0]; // move child 1 up
if (parent->child[1]->data[1]) // child 1 has 2 data
{
parent->child[1]->data[0] = parent->child[1]->data[1];
parent->child[1]->data[1] = NULL;
return 1;
}
// child-1 has 1 data
if (parent->data[1]) // parent has 2 data
{
parent->child[1]->data[0] = parent->data[1]; // move data 1 down
parent->data[1] = parent->child[2]->data[0]; // move child 2 data 0 up
if (parent->child[2]->data[1]) // child 2 has 2 data
{
parent->child[2]->data[0] = parent->child[2]->data[1];
parent->child[2]->data[1] = NULL;
}
else // child 2 has 1 data, parent has 2 data, move data 1 down to child 1
{
delete parent->child[2];
parent->child[2] = NULL;
parent->child[1]->data[1] = parent->data[1];
parent->data[1] = NULL;
}
return 1;
}
// not yet done (only data 0 and child 1 data 0)
// move data 0 down
// conbine two data to one node
parent->child[0]->data[1] = parent->data[0];
delete parent->child[1];
node23<Type> *del = parent;
parent = parent->child[0];
delete del;
return 0;
}
else if (!(parent->child[1]->data[0])) // child 1 is empty
{
if (parent->child[0]->data[1]) // child 0 has 2 data
{
parent->child[1]->data[0] = parent->data[0];
parent->data[0] = parent->child[0]->data[1];
parent->child[0]->data[1] = NULL;
return 1;
}
// child 0 has 1 data
if (parent->data[1]) // parent has 2 data
{
if (parent->child[2]->data[1]) // parent child 2 has 2 data
{
parent->child[1]->data[0] = parent->data[1];
parent->data[1] = parent->child[2]->data[0];
parent->child[2]->data[0] = parent->child[2]->data[1];
parent->child[2]->data[1] = NULL;
}
else // parent child 2 has 1 data
{
parent->child[1]->data[0] = parent->data[1];
parent->child[1]->data[1] = parent->child[2]->data[0];
parent->data[1] = NULL;
delete parent->child[2];
parent->child[2] = NULL;
}
return 1;
}
// not yet done (only data 0 and child 0 data 0)
// move data 0 down
// conbine two data to one node
parent->child[0]->data[1] = parent->data[0];
delete parent->child[1];
node23<Type> *del = parent;
parent = parent->child[0];
delete del;
return 0;
}
else // child 2 is empty, parent has 2 data
{
if (parent->child[1]->data[1]) // parent child 1 has 2 data
{
parent->child[2]->data[0] = parent->data[1];
parent->data[1] = parent->child[1]->data[1];
parent->child[1]->data[1] = NULL;
}
else // parent child 1 has 1 data
{
parent->child[1]->data[1] = parent->data[1];
parent->data[1] = NULL;
delete parent->child[2];
parent->child[2] = NULL;
}
return 1;
}
}
else // last node
{
delete parent;
parent = NULL;
return 1;
}
}
/*
After distribution, not done yet, do node merging
return 1 if is done here
return 0 if not done yet
Return whether all the works has been done
*/
template<class type>
bool Tree23_merge(node23<Type>* &parent, node23<Type>* root)
{
if (parent == root)
return 1;
if (parent->child[0] == root) // node need to merge from child 0
{
if (parent->child[1]->data[1]) // child 1 has 2 data
{
node23<Type>* child0 = new node23<Type>;
child0->data[1] = NULL;
child0->child[2] = NULL;
child0->child[0] = parent->child[0];
parent->child[0] = child0;
child0->child[1] = parent->child[1]->child[0];
child0->data[0] = parent->data[0];
parent->data[0] = parent->child[1]->data[0];
parent->child[1]->data[0] = parent->child[1]->data[1];
parent->child[1]->data[1] = NULL;
parent->child[1]->child[0] = parent->child[1]->child[1];
parent->child[1]->child[1] = parent->child[1]->child[2];
parent->child[1]->child[2] = NULL;
return 1;
}
else if (parent->data[1]) // child 1 has 1 data, parent has 2 data
{
parent->child[1]->data[1] = parent->child[1]->data[0];
parent->child[1]->data[0] = parent->data[0];
parent->child[1]->child[2] = parent->child[1]->child[1];
parent->child[1]->child[1] = parent->child[1]->child[0];
parent->child[1]->child[0] = parent->child[0];
parent->data[0] = parent->data[1];
parent->data[1] = NULL;
parent->child[0] = parent->child[1];
parent->child[1] = parent->child[2];
parent->child[2] = NULL;
return 1;
}
else // child 1 has 1 data, parent has 1 data
{
node23<Type> *del = parent->child[1];
parent->data[1] = del->data[0];
parent->child[1] = del->child[0];
parent->child[2] = del->child[1];
delete del;
return 0; // height reduced, not done
}
}
else if (parent->child[1] == root) // node need to merge from child 1
{
if (parent->child[0]->data[1]) // child 0 has 2 data
{
node23<Type>* child1 = new node23<Type>;
child1->data[1] = NULL;
child1->child[2] = NULL;
child1->child[1] = parent->child[1];
child1->child[0] = parent->child[0]->child[2];
parent->child[1] = child1;
child1->data[0] = parent->data[0];
parent->data[0] = parent->child[0]->data[1];
parent->child[0]->data[1] = NULL;
parent->child[0]->child[2] = NULL;
return 1;
}
else if (parent->data[1]) // child 0 has 1 data, parent has 2 data
{
parent->child[0]->data[1] = parent->data[0];
parent->data[0] = parent->data[1];
parent->data[1] = NULL;
parent->child[0]->child[2] = parent->child[1];
parent->child[1] = parent->child[2];
parent->child[2] = NULL;
return 1;
}
else // child 0 has 1 data, parent has 1 data
{
node23<Type> *del = parent->child[0];
parent->data[1] = parent->data[0];
parent->data[0] = del->data[0];
parent->child[2] = parent->child[1];
parent->child[1] = del->child[1];
parent->child[0] = del->child[0];
delete del;
return 0; // height reduced, not done
}
}
else // node need to merge from child 2
{
if (parent->child[1]->data[1]) // child 1 has 2 data
{
node23<Type>* child2 = new node23<Type>;
child2->data[1] = NULL;
child2->child[2] = NULL;
child2->child[1] = parent->child[2];
parent->child[2] = child2;
child2->child[0] = parent->child[1]->child[2];
parent->child[1]->child[2] = NULL;
child2->data[0] = parent->data[1];
parent->data[1] = parent->child[1]->data[1];
parent->child[1]->data[1] = NULL;
return 1;
}
else // child 1 has 1 data, parent has 2 data
{
parent->child[1]->data[1] = parent->data[1];
parent->data[1] = NULL;
parent->child[1]->child[2] = parent->child[2];
parent->child[2] = NULL;
return 1;
}
}
}